学院首页> 师资队伍> 硕士生导师> 正文

吴群英教授

一、 基本情况

吴群英，女，1961年生，博士、教授，硕士生导师。现为广西壮族自治区优秀专家、“广西新世纪十百千人才工程”第二层次人选、广西高校百名中青年学科带头人、广西区优秀教师、广西区教学名师、中国工程概率统计学会理事、广西数学学会常务理事、广西统计学会理事。

联系地址：广西桂林市建干路12号，桂林理工大学 williamhill体育入口注册 （邮编：541004）

联系电话：0773-5896178

电子邮址：wqy666@glut.edu.cn

二、 个人主要经历

  1. 1982.7～1985.9 桂林工学院数学教研室任教

  2. 1985.9～1987.7 浙江大学数学系读研究生(概率论与数理统计专业)

  3. 1987.7～2000.9 桂林工学院基础部数学教研室任教

  4. 2000.9～2003.6 中南大学读博士(概率论与数理统计专业)、桂林工学院基础部数学教研室任教

  5. 2003.6～至今 桂林理工大学williamhill体育入口注册统计学教研室任教

三、 主要荣誉奖励

  1. 2007年获广西壮族自治区优秀专家

  2. 2006年入选“广西新世纪十百千人才工程”第二层次人选

  3. 2005年入选“广西高校百名中青年学科带头人”

  4. 2009年获自治区优秀教师，并给予记个人二等功

  5. 2011年获广西高等学校教学名师奖

  6. 2007年获广西高等学校优秀共产党员

  7. 2009年获广西高等学校优秀共产党员

  8. 2006年获广西科技进步奖二等奖，排名第1

  9. 2014年获广西自然科学奖三等奖，排名第1

  10. 2012年广西高等教育自治区级教学成果奖一等奖，排名第1

  11. 2009年广西高等教育自治区级教学成果二等奖，排名第1

  12. 2017年广西高等教育自治区级教学成果奖二等奖，排名第2

  13. 2008～2009年度桂林市劳动模范荣誉称号

  14. 2005年获湖南省优秀博士学位论文奖

  15. 2009年负责统计学教学团队获广西高校自治区级教学团队

  16. 2007年负责线性代数课程获广西高校自治区级精品课程

  17. 2008年负责统计学课程获广西高校自治区级精品课程

  18. 2006年获21世纪第二届广西高等学校优秀教材二等奖，排名第1

  19. 2011年，独著教材《随机过程》获2006—2008年广西高等学校优秀教材二等奖

四、主要研究项目

国家级科研项目

  1. 有限阶矩检验统计量及其极限理论研究，主持，国家自然科学基金，项目批准号：11661029，时间：2017.01~2020.12

  2. 纵向数据变系数模型非参数估计的极限理论研究，主持，国家自然科学基金,项目批准号：11361019,时间:2014.01~2017.12

  3. 线性和部分线性模型的M估计研究，主持，国家自然科学基金，项目批准号：11061012，时间：2011.1～2013.12；

  4. 从广义生灭过程到一般马氏过程的若干问题研究，主持，国家自然科学基金，项目批准号：10661006，时间：2007.1~2009.12。

  5. 单指标变系数模型两类惩罚估计量的极限理论研究，主持，国家自然科学基金，项目批准号：12061028，时间：2021.01~2024.12

省级科研项目

  1. 从广义生灭过程到一般马氏过程的若干问题研究，主持，广西“新世纪十百千人才工程”专项基金资助，资助批准号：2005214号；时间：2007.3~2009.12

  2. 统计数据分析与信息处理技术获第四批广西高校人才小高地资助创新团队，创新团队带头人，桂教人〔2011〕47号，时间：2012.1-2014.12

  3. 随机过程正交熵方法的研究，主持，广西高校百名中青年学科带头人资助计划项目，桂教人[2005]64号，时间：2005.10~2007.12

  4. 非参数估计方法的概率极限理论及其在经济的应用研究，广西基金重点项目，项目编号：2013GXNSFDA019001，时间：2013.04.01~2016.03.31

  5. 若干类随机变量函数的几乎处处中心极限定理的研究，广西基金面上项目，项目编号：2015GXNSFAA139008，时间：2015.04.01 ~2018.03.31

  6. 自正则和极限理论及其在空间信息中的应用，主持，广西自然科学基金，项目编号：2012GXNSFAA053010，时间：2012.4.1~2015.3.1

  7. 部分线性模型的M估计研究及其在经济、金融中的应用，主持，广西自然科学基金，项目编号：2010GXNSFA013120，时间：2010.3.1~2013.3.31

  8. 混合随机变量的极限理论及其在经济、金融中的应用，主持，广西自然科学基金，项目编号：桂科自0728212，时间：2007.05.1~2010.05.31

  9. 马尔可夫骨架过程与风险决策理论，主持，广西自然科学基金，项目编号：桂科自0339071，时间：2003.07.1~2006.07.1

  10. GIS与测绘数据处理、建模及其应用研究，主持，广西空间信息与测绘重点实验室主任基金，项目编号：桂科能1103108-08，时间：2012.1~2013.12

省级教改项目

  1. 基于一级学科统计学专业教学整体优化的研究与实践，主持，2012年度新世纪广西高等教育教学改革工程立项项目，广西高校教学名师，桂教高教（2012）25号，项目编号：2012GXMS183，时间：2012.4~2013.12

  2. 统计学专业课程体系和教学模式的改革研究与实践，主持，广西新世纪高等教育教学教改工程“十一五”第二批资助项目，桂教高教[2006]194号B76，时间：2006.09~2008.10

  3. 应用统计广西高校重点实验室，实验室主任，桂教科研〔2014〕6号，2014.4.15

  4. 统计学广西重点学科，学科带头人，桂教科研[2013] 16号，2013.7.31

  5. 统计学2014年高等学校优势特色专业建设点，专业负责人，桂教高教（2014）52号，广西教育厅，2014.7.14

  6. 统计学专业获广西高等学校特色专业及课程一体化建设项目，项目负责人，类型：优势，项目编号：GXTSZY213，广西壮族自治区教育厅，桂教高教[2011]102号, 2011.9.14

  7. 应用统计硕士2014年自治区财政资助的专业学位授权点建设项目，项目负责人，桂学位〔2014〕3号，2014.4.1

  8. 统计学广西高校自治区级教学团队，团队负责人，广西壮族自治区教育厅，桂教高教[2009]153号；2009.10

  9. 自治区级精品课程线性代数，主持，新世纪教改工程立项项目，桂教高教〔2007〕111号，时间：2007.8~2010.8

  10. 自治区级精品课程统计学主持，新世纪教改工程立项项目，桂教高教〔2008〕178号，项目编号：002401303065，时间：2008.8-2011.8

五、 已出版的专著和教材

  1. 吴群英，《广义生灭过程》，科学出版社，2004.8

  2. 吴群英，《混合序列的概率极限理论》，科学出版社，2006.3

  3. 吴群英，林亮，《应用数理统计》，天津大学出版社，2004.9

  4. 吴群英，《随机过程》，华中师范大学出版社，2008.8

  5. 林亮，吴群英，王远清，徐海云，涂雄苓，何宝珠，刘筱萍，《统计实验》，国防工业出版社，2006.9

六、 近期发表的科研论文

  1. Qunying Wu, Yuanying Jiang*, Strong law of large numbers and Chover’s law of the iterated logarithm under sub-linear expectations, Journal of Mathematical Analysis and Applications，2018，460(1)：252–270，WOS: 000423247600016，IDS: FT6ER，https://doi.org/10.1016/j.jmaa.2017.11.053

  2. Qunying Wu*, Yuanying Jiang, Almost sure convergence for self-normalized products of sums of partial sums of 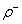-mixing sequences，Filomat, 2019, 33(8): 2471–2488，WOS: 000496946500024，IDS: JN5OB

  3. Qunying Wu*，Jianfang Lu，Another form of Chover’s law of the iterated logarithm under sub-linear expectations，Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas，2020, 114 (1): 1-22 WOS: 000512375200001，IDS: KJ9LF

  4. Qunying Wu，Precise asymptotics for complete moment convergence under sub-linear expectations，Mathematical Problems in Engineering，2020，Volume 2020, Article ID 3145935, 13 pages，https://doi.org/10.1155/2020/3145935， WOS: 000536806000010，IDS: LT0ZX

  5. Qunying Wu*, Yuanying Jiang, Complete convergence and complete moment convergence for negatively dependent random variables under sub-linear expectations, Filomat, 2020, 34 (4): 1093–1104，WOS: 000600790800005，IDS: PI0KY，https://doi.org/10.2298/FIL2004093W

  6. Qunying Wu，Complete Convergence for END Random Variables under Sublinear Expectations，Discrete Dynamics in Nature and Society，Volume 2021, Article ID 5529109, 10 pages，WOS: 000668937700002，IDS：TC9DP，https://doi.org/10.1155/2021/5529109

  7. Qunying Wu，Strong limit theorems of weighted sums for extended negatively dependent random variables under sub-linear expectations，Communications in Statistics-Theory and Methods，2023, 52(12): 4356-4368，WOS: 000710384000001，IDS：WL4NP，DOI: 10.1080/03610926.2021.1993259

  8. Qunying Wu，Convergence of series and almost sure convergence for weighted random variables under sub-linear expectations, Filomat, 2023, 37 (2): 615-626, WOS: 000964694700022, https://doi.org/10.2298/FIL2302615W

  9. Qunying Wu，The convergence rate for the laws of logarithms under sub-linear expectations, AIMS MATHEMATICS, 2023, 8(10): 24786-24801, WOS: 001097508000005, IDS: X3LR4, DOI: 10.3934/math.20231264

  10. Qunying Wu, Yuanying Jiang*，Almost Sure Central Limit Theorem for Self-Normalized Partial Sums of Negatively Associated Random Variables，Filomat，2017，31:5，1413–1422，SCI检索号：EQ3TR

  11. Qunying Wu and Xiang Zeng*，Equivalent conditions of complete moment convergence for extended negatively dependent random variables，Journal of Inequalities and Applications，(2017) 2017:125 DOI 10.1186/s13660-017-1403-2，SCI检索号：EW8MQ

  12. Qunying Wu and Yuanying Jiang，Some limiting behavior for asymptotically negative associated random variables，Probability in the Engineering and Informational Sciences, page 1 of 9, 2017. doi:10.1017/S0269964816000437，SCI

  13. Feng Xu , Qunying Wu*，Almost sure central limit theorem for self-normalized partial sums of  -mixing sequences，Statistics and Probability Letters，2017，(129)：17–27，SCI

  14. Qunying Wu,Further study complete convergence for weighted sums of PNQD Random Variables，Journal of Inequalities and Applications，2015，2015:289，DOI 10.1186/s13660-015-0814-1，SCI检索号：CS0FZ

  15. Qunying Wu，Yuanying Jiang，Almost sure central limit theorem for self-normalized partial sums and maxima，Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A-Matemáticas, 2016，110(2): 699–710, SCI检索号：DT6FJ

  16. Qunying Wu，Almost sure central limit theorem for self-normalized products of partial sums of negatively associated sequences，Communications in Statistics-Theory and Methods，2017，46（6）：2593-2606，SCI检索号：EI3TH

  17. Qunying Wu，Laws of the iterated logarithm for ρ-mixing random variables with normal distribution, Acta Mathematicae Applicatae Sinica，English Series，2016，32(2): 385-394, SCI检索号：DK9EN

  18. Qunying Wu and Yuanying Jiang*, Complete convergence and complete moment convergence for negatively associated sequences of random variables，Journal of Inequalities and Applications，2016，2016:157 DOI 10.1186/s13660-016-1107-z，SCI检索号：DQ2JQ

  19. Qunying Wu，An extension of almost sure central limit theorem for the maximum of stationary Gaussian random fields，Communications in Statistics-Theory and Methods，2017，46（8）：3667-3675 , SCI检索号：JCR4区

  20. Qunying Wu and Yuanying Jiang*, Complete moment convergence for negatively dependent sequences of random variables, Discrete Dynamics in Nature and Society，2016，Volume 2016, Article ID 9039345, 6 pages，SCI检索号：DT0FC

  21. Qunying Wu, Improved results in almost sure central limit theorems for the maxima and partial sums for Gaussian sequences，Journal of Inequalities and Applications, 2015:109，DOI 10.1186/s13660-015-0634-3，SCI检索号：CM0ZM

  22. 吴群英，正常返Markov链的几乎处处中心极限定理，中国科学:数学2015，45(5): 663~670

  23. Xiang Zeng and Qunying Wu*，The improved results in almost sure centrallimit theorem for the maxima of strongly dependent stationary Gaussian vectorsequences，Journal of Inequalities andApplications，2015: 224 DOI10.1186/s13660-015-0740-2，SCI检索号： CR7WY

  24. Qunying Wu, Generalized weak invariance principle for products of partial sums of random variables,Chinese Journal of Contemporary Mathematics, 2014, 35(2)：193-200

  25. 吴群英，随机变量部分和乘积的广义弱不变原理，数学年刊，2014， 35A （2）：225~234

  26. Dehua Qiu, Qunying Wu andPingyan Chen，Complete convergence for negatively orthant dependent random variables，Journal of Inequalities and Applications，2014, 2014: 145，SCI检索号：AK2BM

  27. Qunying Wu, Pingyan Chen, An improved result in almost sure central limit theory for self-normalized products of partial sums, Journal of Inequalities and Applications, 2013, 2013: 129 doi:10.1186/1029-242X-2013-129，SCI检索号：207AP .

  28. Qunying Wu, Pingyan Chen, Strong representation results of Kaplan-Meier estimator for censored NA data，Journal of Inequalities and Applications 2013 2013:340，doi:10.1186/1029-242X-2013-340，SCI检索号：217QZ

  29. Qunying Wu, Pingyan Chen, A Berry-Esseen Type Bound in Kernel Density Estimation for Negatively Associated Censored Data，Journal of Applied Mathematics，Volume 2013, Article ID 541250, 9 pageshttp://dx.doi.org/10.1155/2013/541250，SCI检索号：215GZ

  30. Qunying Wu，Yuanying Jiang，The strong consistency of estimator in linear model for negatively dependent random samples, Communications in Statistics–Theory and Methods, 2011, 40(03): 467-491， SCI检索号：680HK，EI检索号：20104813428918

  31. Qunying Wu，Yuanying Jiang，The strong law of large number for pairwise NQD random variables，Journal of Systems Science and Complexity，2011，24(2): 347–357 SCI检索号：750FG.

  32. Qunying Wu，An almost sure central limit theorem for the weight function sequences of NA random variables， Proceedings - Mathematical Sciences，2011，121(3)：369-377， ISSN: 0253-4142，SCI检索号: 815CB，EI检索号：20114214446128.

  33. Qunying Wu, A note on the almost sure limit theorem for self-normalized partial sums of random variables in the domain of attraction of the normal law，Journal of Inequalities and Applications 2012, 2012:17，doi:10.1186/1029-242X-2012-17，SCI检索号:935OH

  34. Qunying Wu, A complete convergence theorem for weighted sums of arrays of rowwise negatively dependent random variables，Journal of Inequalities and Applications，2012，doi:10.1186/1029-242X-2012-50，SCI检索号：128BW

  35. Qunying Wu, Almost sure central limit theory for self-normalized products of sums of partial sums, Journal of Applied Mathematics，Volume 2012, Article ID 329391, 13 pages，doi:10.1155/2012/329391，SCI检索号：938AA

  36. Qunying Wu, Almost sure central limit theory for products of sums of partial sums，Applied Mathematics-A Journal of Chinese Universities Series B, 2012, 27(2): 169-180, SCI检索号：958HH

  37. Qunying Wu, A strong limit theorem for weighted sums of sequences of negatively dependent random variables, Journal of Inequalities and Applications, vol. 2010, Article ID 383805, 8 pages, 2010. doi:10.1155/2010/383805. SCI检索号：664HX.

  38. Qunying Wu, Complete convergence for negatively dependent sequences of random variables, Journal of Inequalities and Applications, Volume 2010, Article ID 507293, 10 pages, SCI检索号：598MQ.

  39. Qunying Wu, Yuanying Jiang, A law of the iterated logarithm of partial sums for NA random variables, Journal of the Korean Statistical Society, 2010, 39(2): 199-206. SCI检索号：610AP.

  40. Qunying Wu, Yuanying Jiang, Chover-type laws of the k-iterated logarithm for -mixing sequences of random variables, Journal of Mathematical Analysis and Applications, 2010, 366(2): 435~443 SCI检索号：565KD.

  41. Qunying Wu, Sufficient and necessary conditions of complete convergence for weighted sums of PNQD random variables， Journal of Applied Mathematics，2012，Volume 2012, Article ID 104390, 10 pages，doi:10.1155/2012/104390，SCI检索号：990VP

  42. Qunying Wu, Yuanying Jiang, Chover’s Law of the Iterated Logarithm for NA Sequences, Journal of Systems Science and Complexity, E07258, 2010, 23(2): 293~302, SCI检索号：596YC, EI检索号：20102012946049.

  43. Qunying Wu, An improved result in almost sure central limit theory for the products of partial sums with stable distribution, Chinese Annals of Mathematics, Series B, 2012，33B（6）：919-930，SCI检索号：039LE

  44. Qunying Wu, Further study strong consistency of estimator in linear model for -mixing random samples, Journal of Systems Science and Complexity, 2011，24(5): 969–980, SCI检索号: 829JW，EI检索号: 20114114416100.

  45. Qunying Wu, Yuanying Jiang, Some strong limit theorems for -mixing sequences of random variables, Statistics & Probability Letters, 2008, 78(8): 1017~1023. SCI检索号：313LX.

  46. Qunying Wu, Yuanying Jiang, Some strong limit theorems for weighted product sums of -mixing sequences of random variables, Journal of Inequalities and Applications, Volume 2009, Article ID 174768, 10 pages, doi:10.1155/2009/174768, SCI检索号：540JF.

  47. Qunying Wu, Almost sure limit theorems for stable distribution, Statistics & Probability Letters, 2011, 81 (6): 662–672, SCI检索号：782MS.

  48. Qunying Wu, Complete convergence for weighted sums of sequences of negatively dependent random variables, Journal of Probability and Statistics, vol. 2011, Article ID 202015, 16 pages, 2011. doi:10.1155/2011/202015.

  49. 吴群英，随机变量部分和乘积的广义弱不变原理，数学年刊，2014，35A（2）：225~234

  50. 吴群英, 两两NQD列的收敛性质, 数学学报, 2002, 45(3): 617~624.

  51. Wu Qunying, Zhang Hanjun and Hou Zhenting, An extended birth-death Q-matrix with instantaneous state and catastrophes(I), Chinese Journal of Contemporary Mathematics, 2003, 24(2): 159~168.

  52. 吴群英, 张汉君, 侯振挺, 含瞬时态、具有突变率的广义生-灭Q矩阵(I), 数学年刊(A辑), 2003, 24(2): 187~192.

  53. Wu Qunying, Zhang Hanjun and Hou Zhenting, An extended birth-death Q-Matrix with instantaneous state and catastrophes(II). Chinese Journal of Contemporary Mathematics, 2003, 24(4): 317~328.

  54. 吴群英, 张汉君, 侯振挺, 含瞬时态、具有突变率的广义生-灭Q矩阵(II), 数学年刊(A辑), 2003, 24(5): 555~564.

  55. Wu, Q.Y., Strong consistency of M estimator in linear model for negatively associated samples， Journal of Systems Science and Complexity，2006，19(4): 592~600.

  56. 吴群英, 张汉君, 广义生-灭过程, 系统科学与数学, 2003, 23(4): 517~528.

  57. 吴群英, 王岳宝, 独立阵列和的最大值完全收敛的等价条件, 系统科学与数学, 2002, 22(2): 192~199.

  58. 吴群英, Q过程的 -不变测度——含吸收态情形, 数学物理学报, 2004, 24A(1): 16~25.

  59. 吴群英, 混合线性模型M估计的强相合性, 数学物理学报, 2005, 25A(1): 41-46.

  60. 吴群英, 不同分布 混合序列的强收敛速度, 数学研究与评论, 2004, 24(1): 173~179.

  61. 吴群英，广义生灭最小Q过程的可配称性, 数学研究与评论, 2006，26(4): 769~776.

  62. 吴群英, Q过程的 不变测度, 应用概率统计, 2003, 19(4): 394~400.

  63. 吴群英, 王远清, 伍艳春, NA阵列行和最大值的若干极限定理, 应用概率统计, 2006, 22(1):56~62.

  64. 吴群英, 混合序列的若干收敛性质, 工程数学学报, 2001,18(3): 58~64,50.

  65. 吴群英, 广义生灭过程—强遍历性, 工程数学学报, 2002,19(1): 104~108.

  66. 吴群英, 人口过程——遍历性及指数遍历性, 工程数学学报, 2003, 20 (1):119~122.

  67. 吴群英, 林亮, 混合序列的完全收敛性和强收敛性, 工程数学学报, 2004, 21(1): 75~80.

  68. WU Qun-ying, The minimal Q-process and its properties for an extended birth-death Q-matrix, Mathematica Applicata, 2002, 15(4): 79~84.

  69. 吴群英, 人口过程——唯一性与常返性, 应用数学, 2001, 14(4): 51~54.

  70. 吴群英, 混合序列加权和的完全收敛性和强收敛性, 应用数学, 2002, 15(1):1~4.

  71. 吴群英, 混合、 混合、 混合线性模型M估计的强相合性, 应用数学, 2004, 17(3): 393~397.

  72. WU Qun-ying, Almost Sure Convergence for -mixing Random Variable Sequences, Mathematica Applicata, 2008, 21(4):629~634.

  73. 吴群英, Q过程的 -不变向量, 应用数学, 2001, 14:57~61.

  74. WU Qun-ying, An extended birth-death processes with catastrophes——stochastically monotone, Feller and symmetric properties, Chinese quarterly Journal of Mathematics, 2002,17(2): 36~42.

  75. WU Qun-ying, A note of the uniqueness criterion for single birth processes, Chinese quarterly Journal of Mathematics, 2002,17(3): 88~92.

  76. WU Qun-ying, On Kendall’s conjecture for an extended birth-death Q-processes with instantaneous state and catastrophes. Chinese quarterly Journal of Mathematics, 2004, 19(1): 41~46

  77. 吴群英, 广义分枝过程的强遍历性, 纯粹数学与应用数学, 2002, 18(3): 211~214.

  78. 吴群英, -混合序列的不变原理, 纯粹数学与应用数学, 2003, 19(1): 12~15.

  79. 吴群英 林亮, 广义生-灭最小Q过程的常返、遍历性, 纯粹数学与应用数学, 2007, 23(3): 289-292.

  80. 吴群英, 王远清, 混合阵列行和的若干极限定理, 纯粹数学与应用数学, 2007, 23(4):458-462.

  81. 吴群英, 两两NQD列的广义Jamison型加权和的强收敛性, 数学研究, 2001, 34(4): 386~393.

七、 近期发表的教改论文

  1. 吴群英，蒋远营，张浩敏，王想，王彬，邓光明，大数据背景下应用统计学专业改革探讨，教育教学论坛，2016，43：101-103 

  2. 吴群英，蒋远营，张浩敏，王想，王彬，邓光明，互联网融合下构建新的统计学专业课程体系的改革与实践，高教学刊，2016,18：129-130

  3. 吴群英、林亮、徐海云、邓光明、王远清，开创“应用性、实验性、案例性”一体化的统计学专业课程体系和教学模式，桂林理工大学学报, 2010，30(高教研究专辑)：122-125

  4. 吴群英, 邓光明, 概率论与数理统计在统计学专业的基础地位的探讨与实践, 现代学术研究杂志, 2008, 19(3): 63~64.

  5. 吴群英, 林亮, 邓光明, 关于统计学教育的思考、改革和实践, 高校教育研究, 2008, 5: 206~207

  6. 吴群英, 蒋远营, 林亮, 王远清, 统计学专业改革探讨, 桂林工学院学报, 2008, 28(高教研究专辑): 45~47

  7. 吴群英, 唐国强, 梁鹏, 关于数学实验系列课程与创新人才培养的思考、改革和实践, 科学时代, 2010, (5) : 172~173

  8. 吴群英, 梁鹏, 唐国强, 在高等数学教学中融入数学实验的改革和实践, 扬州大学学报, 2010, 14(6): 159~160

八、 指导研究生发表的主要论文

  1. Lizhen Huang & Qunying Wu*，Complete convergence for weighted sums of widely negative orthant dependent random variables under the sub-linear expectations，Communications in Statistics - Theory and Methods, 2024. 2. 21，WOS: 001378477000001，DOI: 10.1080/03610926.2024.2307454，

  2. Baozhen Wang and Qunying Wu*，Almost sure convergence for a class of dependent random variables under sub-linear expectations，AIMS Mathematics, 2024，9(7): 17259–17275，WOS: 001229138800004，doi: 10.3934/math.2024838

  3. Lunyi Liu & Qunying Wu*，Complete convergence theorems for weighted sums of extended negatively dependent random variables under sub-linear expectations，Communications in Statistics - Theory and Methods，2024.6.30，WOS：001258006300001，DOI: 10.1080/03610926.2024.2366910，

  4. Lunyi Liu and Qunying Wu*，Complete integral convergence for weighted sums of negatively dependent random variables under sub-linear expectations，AIMS Mathematics，2023, 8(9): 22319–22337，WOS: 001031576900013, DOI: 10.3934/math.20231138

  5. Lizhen Huang, Qunying Wu*, Precise asymptotics for complete integral convergence in the law of the logarithm under the sub-linear expectations，AIMS Mathematics，2023, 8(4): 8964-8984. WOS: 000936575200010, DOI: 10.3934/math.2023449

  6. Li Wang & Qunying Wu*，Complete convergence and complete integral convergence for weighted sums of widely negative dependent random variables under the sub-linear expectations，Communications in Statistics - Theory and Methods，2024, 53 (10): 3599–3615, WOS: 000899347700001，DOI: 10.1080/03610926.2022.2158343

  7. Chengcheng Jia & Qunying Wu*，Complete convergence and complete integral convergence for randomly weighted sums under the sublinear expectations，Communications in Statistics - Theory and Methods，2024, 53(13): 4790-4804, WOS: 000964096100001, DOI: 10.1080/03610926.2023.2195029

  8. Chengcheng Jia & Qunying Wu*，Complete convergence for weighted sums of widely negative dependent random variables under the sub-linear expectations, Communications in Statistics - Theory and Methods，2024, 53(14): 5018–5040, WOS:000972930000001, DOI: 10.1080/03610926.2023.2203283

  9. Xiaocong Chen and Qunying Wu*，Complete convergence theorems for moving average process generated by independent random variables under sub-linear expectations，Communications in Statistics - Theory and Methods，2024, 53(15): 5378–5404，WOS:001002498600001, DOI: 10.1080/03610926.2023.2220449

  10. Xiaocong Chen and Qunying Wu*，Further research on complete integral convergence for moving average process of ND random variables under sub-linear expectations, Communications in Statistics - Theory and Methods, 2024，53(19), 7102–7118. WOS: 001068318800001, DOI: 10.1080/03610926.2023.2258428

  11. Zhouting Zhan & Qunying Wu*，Strong laws of large numbers for weighted sums of extended negatively dependent random variables under sub-linear expectations，Communications in Statistics - Theory and Methods，WOS:000613817300001，IDS : QB0EY，https://doi.org/10.1080/03610926.2021.1873380

  12. Rong Hu & Qunying Wu*，Complete convergence theorems for arrays of row-wise extended negatively dependent random variables under sub-linear expectations，Communications in Statistics - Theory and Methods，2023，52(21): 7669-7683，WOS: 000771227600001，DOI: 10.1080/03610926.2022.2051050

  13. Binxia CHEN, Qunying WU*，The laws of large numbers for Pareto-type random variables under sub-linear expectation，Front. Math. China 2022, 17(5): 783–796，WOS: 000914712100003, DOI: 10.1007/s11464-022-1026-x

  14. Chengcheng Jia and Qunying Wu*，Complete convergence and complete integral convergence for weighted sums of widely acceptable random variables under the sub-linear expectations，AIMS Mathematics, 2022，7(5): 8430–8448，WOS: 000764882400001，DOI: 10.3934/math.2022470

  15. Xiaocong Chen and Qunying Wu*，Complete convergence and complete integral convergence of partial sums for moving average process under sub-linear expectations，AIMS Mathematics, 2022，7(6): 9694–9715，WOS: 000771919300010，DOI: 10.3934/math.2022540

  16. Li Wang and Qunying Wu∗ Almost sure convergence theorems for arrays under sub-linear expectations，AIMS Mathematics, 2022，7(10): 17767–17784，WOS: 000837418700002，DOI:10.3934/math.2022978

  17. Li Wang & Qunying Wu*，Complete integral convergence for weighted sums of widely negative dependent random variables under the sub-linear expectations，Communications in Statistics-Theory and Methods，2023，52 (24): 8763-8784，WOS: 000794907400001，DOI: 10.1080/03610926.2022.2071448，

  18. Shuyan Li and Qunying Wu∗，Complete integration convergence for arrays of rowwise extended negatively dependent random variables under the sub-linear expectations，AIMS Mathematics, 2021，6(11): 12166–12181，WOS: 000697908400026，IDS：UT1UO，DOI: 10.3934/math.2021706，

  19. Rong Hu and Qunying Wu*，Complete Convergence for Weighted Sums of Widely Acceptable Random Variables under Sublinear Expectations，Discrete Dynamics in Nature and Society，Volume 2021, Article ID 5526609, 10 pages，WOS: 000659053800001，IDS:  SO6AX，https://doi.org/10.1155/2021/5526609，

  20. Ziwei Liang and Qunying Wu*，Several different types of convergence for nd random variables under sublinear expectations，Discrete Dynamics in Nature and Society，Volume 2021, Article ID 6653435, 9 pages，WOS: 000636274500001，IDS：RH5RB， https://doi.org/10.1155/2021/6653435，

  21. Binxia Chen & Qunying Wu*，Complete convergence theorem for negatively dependent random variables under sub-linear expectations，Communications in Statistics - Theory and Methods，2022, 51(10): 3202–3215，WOS:000548941100001，IDS : MK7CD，DOI: https://doi.org/10.1080/03610926.2020.1790603

  22. Jie Li and Qunying Wu*, Complete integral convergence for arrays of row-wise extended independent random variables under Sub-linear expectations，Communications in Statistics - Theory and Methods，2020, 49(22): 5613-5626, WOS: 000471455400001，IDS: ID1QK https://doi.org/10.1080/03610926.2019.1620954

  23. Ziwei Liang and Qunying Wu*，Theorems of complete convergence and complete integral convergence for END random variables under sub-linear expectations，Journal of Inequalities and Applications，(2019) 2019:114，IDS: HV7ZG

  24. Xiaochen Ma and QunyingWu*，On Some Conditions for Strong Law of Large Numbers for Weighted Sums of END Random Variables under Sublinear Expectations，Discrete Dynamics in Nature and Society，Volume 2019, Article ID 7945431, 8 pages，WOS: 000465256400001，IDS: HU4OX，https://doi.org/10.1155/2019/7945431，

  25. Wenjuan Wang & Qunying Wu*，Complete convergence for arrays of row-wise ND random variables under sub-linear expectations, Communications in Statistics -Theory and Methods, 2019, 48:13, 3165-3176，WOS: 000476533200001，IDS: IK4BX，DOI: 10.1080/03610926.2018.1476711

  26. Ruixue Wang and Qunying Wu* Some Types of Convergence for Negatively Dependent Random Variables under Sublinear Expectations, Discrete Dynamics in Nature and Society, Volume 2019, Article ID 9037258, 7 pages, WOS: 000455759300001，IDS: HH5II，https://doi.org/10.1155/2019/9037258

  27. Donglin Yu & Qunying Wu*，Complete convergence for weighted sums of extended negatively dependent random variables under sub-linear expectation，Communications in Statistics - Theory and Methods，2018,47(19): 4741-4750, WOS: 000444437300007，IDS : GT3XK，DOI: 10.1080/03610926.2018.1445860

  28. 余东林;吴群英*; 次线性期望空间下同分布ND列的完全收敛性，桂林理工大学学报，2018，38(3)：593-596

  29. 余东林，吴群英*，Marcinkiewicz type complete convergence for weighte sums under sub-linear expectations，中国科学技术大学学报，2018,48(2)：89-96

  30. 张亚运，吴群英，NA序列的重对数矩收敛的精确渐近性，数学学报，2018,61(3)：403-410，2018.5

  31. 郝晓春，吴群英*，强混合序列加权和及部分和之和乘积的几乎处处中心极限定理的推广，桂林理工大学学报，2018，38(1)：150-154

  32. 梁海业，吴群英*，次线性期望空间下广义ＮＤ列加权和的完全收敛性，中国科学技术大学学报，2018,48(8)：637-642

  33. 马晓晨，吴群英*，次线性期望空间下END列加权和的完全收敛性，应用数学，2019, 32(3): 669-675

  34. 王瑞雪，吴群英*，次线性期望空间下行END阵列的完全积分收敛性，应用数学，2019，32(1): 234-241

  35. 王文娟，吴群英*，Almost Sure Convergence of Weighted Sums for Extended Negatively Dependent Random Variables Under Sub-Linear Expectations，应用数学，2019, 32(2): 382-391

  36. 钟豪媛，吴群英*，次线性期望空间下广义ND序列的强大数定律，桂林理工大学学报，2019,39（2）：524-528

  37. 李婕，吴群英*，次线性期望下ND序列的完全收敛与完全积分收敛，吉林大学学报(理学版)，2019，57(2)：305-310

  38. 唐荣秀，吴群英*，次线性期望下行END阵列的完全积分收敛性，武汉大学学报（理学版），2019，65（6）：609-615

  39. 马晓晨，吴群英*，Limiting Behavior of Weighted Sums of Extended Negatively Dependent Random Variables under Sublinear Expectations，数学进展，2020, 49 (4)：497-511

  40. 邓小芹，吴群英*，ρ-混合序列完全矩收敛的精确渐近性，山东大学学报( 理学版) 2020，55 (6): 32-40

  41. 陈滨霞，吴群英*，次线性期望下独立同分布序列的一般强收敛性，应用数学，2020, 33(3): 718-727

  42. 李书燕，吴群英*，次线性期望空间下END阵列加权和的完全积分收敛，武汉大学学报(理学版)2021，67(2)：165~172

  43. 梁自威，吴群英，Complete Choquet Integral Convergence under Sub-linear Expectations，数学进展，2021.7，2021, 50(2)：629-640

  44. 占周婷，吴群英*，次线性期望空间下行END阵列的完全收敛性，应用数学，2021, 34(1): 65-72

  45. 张冰冰，吴群英*，次线性期望下具有随机系数相依线性过程的完全积分收敛性，吉林大学学报（理学版），2021, 59 (2): 271-278

  46. 张冰冰，吴群英*，次线性期望空间下随机加权ND序列的完全积分收敛，武汉大学学报（理学版），2021.6, 2021，67 (3): 270-276

  47. 胡蓉，吴群英* 次线性期望空间下END列加权和的几乎处处收敛性，吉林大学学报（理学版），2021，59(3): 531-536

  48. 陈滨霞，吴群英*，次线性期望下Pareto型随机变量的大数定律[J]. 数学进展，2022, 51(1): 143-164

  49. 陈晓聪、吴群英*，次线性期望空间下END阵列加权和的完全收敛性，应用数学，2022, 35（3）：586-592

  50. 王丽，吴群英*, 次线性期望下随机加权END序列的完全积分收敛, 武汉大学学报（理学版）, 2022, 68(5): 553~561

  51. 嘉程程，吴群英*，次线性期望空间下END序列加权和的完全收敛性，山东大学学报（理学版），2022,57（10）：79-87

  52. 胡蓉，吴群英*，次线性期望下WA随机变量序列加权和的完全收敛性，数学进展，2022, 51(6): 1132-1144

  53. 刘伦义，吴群英*，次线性期望空间下END列Jamison型加权和的几乎处处收敛性，吉林大学学报，2023，61(4): 808-814

  54. 黄丽桢, 吴群英*，次线性期望空间下精确渐近性的一般定律，应用数学，2023, 36(4): 845-858

  55. 王宝珍，吴群英*，次线性期望空间下独立同分布序列的一个强大数定律，应用数学，2024, 37(1): 24-30，DOI:10.13642/j.cnki.42-1184/o1.2024.01.002

  56. Yayun Zhang and Qunying Wu*，Moment convergence rates in the law of iterated logarithm for moving average process under dependence，Journal of Inequalities and Applications，(2016) 2016:253，DOI 10.1186/s13660-016-1190-1，SCI检索号：EA4QG

  57. 付宗魁, 吴群英. NA序列自正则加权和的几乎处处中心极限定理[J]. 湖南师范大学学报, 2016，39（5）：89-94

  58. 邓小芹，吴群英*，NA序列完全矩收敛的精确渐近性，山东大学学报(理学版)，2017,52（1）：102-110

  59. 邓小芹，吴群英，Convergence Rates of Complete Moment Convergence on Moving Average Process for  -Mixing Sequence，应用数学，2017, 30(3): 652-664

  60. 张亚运，吴群英，φ－混合移动平均过程完全矩收敛的精确渐近性，吉林大学学报（理学版），2017, 55（1）：61~69

  61. 张亚运，吴群英， -混合序列的重对数律矩收敛的精确渐近性，山东大学学报(理学版)，2017,52（4）：13-20

  62. 付宗魁, 吴群英.  -混合序列矩收敛的渐近性质. 应用数学学报, 2016,39（3）：452-462

  63. 曹阳，吴群英， -混合序列自正则部分和乘积的几乎处处中心极限定理，桂林理工大学学报， 2017，37（1）：208-216

  64. Feng Xu, Qunying Wu，A note on the almost sure central limit theorem for partial sums ofρ−mixing sequences，Applied Mathematics, 2015, 6, 1574-1580

  65. 刘艳萍，吴群英，杨飞，强相依高斯序列最大值几乎处处中心极限定理，湖北大学学报（自然科学版），2015, 37（5）：427~430

  66. 刘艳萍，吴群英，杨飞，高斯随机域最大值的几乎处处中心极限定理，吉林大学学报（理学版），2015, 53 (6)：1145~1150

  67. 曹阳，吴群英，ρ-混合序列部分和之和乘积的几乎处处中心极限定理，吉林大学学报(理学版)，2015，53 (6)：1151~1155

  68. 付宗奎，吴群英，ρ-混合序列完全矩收敛的精确渐进性，湖北大学学报（自然科学版），2015, 37(5)：431~437

  69. 付宗奎，吴群英，独立情形下自正则和的精确渐近性，纯碎数学与应用数学，2015, 31（6）: 596~603

  70. 徐锋，吴群英，ＮＡ列自正则某些部分和乘积的几乎处处中心极限定理，山东大学学报（理学版），2016, 51（2）：50~57

  71. CAO Yang(曹阳), WU Qunying(吴群英)，Almost Sure Central Limit Theorem for Self-normalized Products of Sums of Partial Sums of ρ-mixing Sequences，应用数学，2016, 29(2): 438-450

  72. Jiangfeng Wang，Qunying Wu，Limiting behavior of the maximum of the partial sum for linearly negative quadrant dependent random variables under residual Cesaro alpha-integrability assumption，Journal of Applied Mathematics，Volume 2012, Article ID 735973, 10 pages，doi:10.1155/2012/735973，SCI检索号：924JU

  73. Jiangfeng Wang，Qunying Wu，Central limit theorem for stationary linear processes generated by linearly negative quadrant-dependent sequence，Journal of Inequalities and Applications 2012, 2012:45 doi:10.1186/1029-242X-2012-45，SCI 检索号：760RG

  74. Daxiang Ye, Qunying Wu, Almost sure central limit theorem of product of partial sums for strongly mixing, Journal of Inequalities and Applications, Volume 2011, Article ID 576301, 9 pages doi:10.1155/2011/576301, SCI检索号：760RG

  75. 徐锋，吴群英，NA列部分和乘积的极限理论，湖北大学学报（自然科学版），2015, 37（3）：222~226

  76. 汪园芳，吴群英.优化权重下平稳高斯序列的最大值与部分和的几乎处处中心极限定理[J].湖北大学学报（自然科学版），2015，37（2）：197~200

  77. 汪园芳，吴群英.随优化权重下非平稳高斯序列的几乎处处中心极限定理[J].华侨大学学报（自然科学版），2015, 36（1）：116~120

  78. 兰冲锋，吴群英，Complete Convergence for Weighted Sums of Negatively Dependent RandomVariables，应用数学，2015, 28(1): 57~64

  79. 兰冲锋，吴群英，END样本最近邻密度估计的强相合速度，数学杂志，2015, 35（3）：665~671

  80. 刘振，吴群英，叶彩园，删失样本 混合序列递归核密度估计的逐点强相合性及速度，河北师范大学学报，2014, 35(2)：129-133

  81. 兰冲锋，吴群英，END样本最近邻密度估计的一致强相合速度，吉林大学学报（理学版），2014, 52(3)：494~498

  82. 刘艳萍，吴群英，优化权重下高斯序列最大值几乎处处中心极限定理，山东大学学报（理学版），2014, 49(5)：50~53

  83. 汪园芳，吴群英，随机域最大值几乎处处中心极限定理，湖北大学学报（自然科学版），2014,36（5）：471~475

  84. 施生塔，吴群英，倪展，ND样本最近邻密度估计的一致强相合速度，桂林理工大学学报，2012，32（4）：631-634.

  85. 叶彩园，吴群英，伍欣叶，删失数据下NA样本核密度估计的相合性，山东大学学报（理学版），2013，48（9）：40~45

  86. 叶彩园，吴群英，刘振，删失数据下核密度估计的相合性，华侨大学学报（自然科学版），2013,34（5）:591~595

  87. 刘艳，吴群英，叶彩园，强混合删失数据密度函数估计的r阶相合性，吉首大学学报（自然科学版），2013,34（4）：19-22.

  88. 刘振，吴群英，叶彩园，删失样本 混合序列递归核密度估计的一致强相合性及速度，湖北大学学报，2013,35（4）：408-414

  89. 伍欣叶、吴群英，核实数据下概率密度函数递归核估计的强相合性，暨南大学学报（自然科学版），2013，34（5）：471-474

  90. 曾翔，吴群英，ND样本加权回归函数估计的强相合速度，吉林大学学报（理学版）,2013,51（2）：237-240

  91. 曾翔，吴群英，α-混合序列下核密度估计量的r阶平均相合性，华侨大学学报（自然科学版），2013.34（3）：84-87

  92. 兰冲锋，吴群英，NA序列部分和之和的完全收敛性探讨，统计与决策，2013.14:9-11

  93. 黄海午，王定成，吴群英，彭江艳，两两NQD随机序列的完全收敛性（英），应用概率统计，2013,29（3）：275~286

  94. 施生塔，吴群英，WOD样本下密度函数核估计的强相合性，浙江大学学报（理学版），2014,41（1）：26-28,34

  95. 伍欣叶，吴群英， -混合删失模型中密度函数K-M估计的 -阶相合速度，山东大学学报（理学版），2014,49（1）：105-110.

  96. 王蒋凤，吴群英，Strong laws of large numbers for arrays of rowwise na and lnqd random variables，Journal of Probability and Statistics，Volume 2011, Article ID 708087, 10 pages doi:10.1155/2011/708087

  97. 王蒋凤，吴群英，NA随机变量序列的Chung-Teicher型强大数定律，桂林理工大学学报，2011, 31(3)：467-470

  98. 叶大相，吴群英，部分和乘积的几乎处处中心极限定理，桂林理工大学学报，2011, 31(3)：471-472

  99. 叶大相, 吴群英, A note on the almost sure central limit theorem, Advances and Applications in Statistical Sciences, 2010, 4(1): 79-88

  100. 叶大相, 吴群英, Almost sure central limit theorem of product of sums for independent random variable, Advances and Applications in Mathematical Sciences, 2011, 8(2): 167-175

  101. 彭先豪, 吴群英, 简默，部分和乘积的几乎处处中心极限定理的推广，桂林理工大学学报，2011, 31(1)：156-159

  102. TAN Cheng-liang, WU Qun-ying, HE Yan-mei，Inequalities of Maximum of Partial Sums and Convergence Rates in the Strong Laws for -mixing Random Variables，数学季刊，2011, 26 (1): 114-119

  103. 夏宝飞，吴群英，NA随机变量序列加权和的几乎处处收敛性，桂林理工大学学报，2011,31(3)：463-466

  104. 夏宝飞，吴群英，郭津，行 混合阵列部分和最大值的矩完全收敛性，吉林大学学报（理学版），2012，50（1）：77~80

  105. 郭津，吴群英，夏宝飞， 混合随机变量列 收敛性，华侨大学学报（自然科学版），2012,33（2）：229~231.

  106. 兰冲锋，吴群英，I.I.D.随机变量部分和之和的完全收敛性，吉林大学学报（理学版），2012,50（3）：507~510

  107. 刘艳，吴群英，ND样本最近邻密度估计的一致强相合性，华侨大学学报（自然科学版），2012,33（5）：590~594

  108. 刘永辉，吴群英，ND样本最近邻密度估计的相合性，吉林大学学报（理学版），2012，50（6）：1141~1145

  109. 倪展，吴群英，施生塔，ＮＤ序列下最近邻密度估计的强相合速度，山东大学学报（理学版），2012，47（12）：6~9

  110. 谭成良, 吴群英, 田国华, 行为 混合随机变量阵列加权和的完全收敛性, 山东大学学报(理学版), 2008, 43(6): 87~91

  111. 谭成良, 吴群英, 混合随机场强大数律的收敛速度, 纯粹数学与应用数学, 2009, 25(2): 402~407

  112. 谭成良, 吴群英, 贾贞, 混合序列部分和的几乎处处收敛性, 吉林大学学报(理学版), 2008, 46(4): 623~627

  113. 付艳莉, 吴群英, NA同分布序列加权和的相合性, 吉林大学学报(理学版), 2010, 48(1): 57~62

  114. 付艳莉, 吴群英, 强混合序列部分和之和乘积的几乎处处中心极限定理, 山东大学学报(理学版), 2010, 45(8): 104~108

  115. 陈晓林, 吴群英, 行 混合阵列加权和最大值的完全收敛性, 山东大学学报(理学版), 2010, 45(2): 20~25

  116. 陈晓林, 吴群英, 周德宏. ND随机变量列的指数不等式, 浙江大学学报, 2011, 38(1): 31-37

  117. 陈晓林, 吴群英, 邓光明, 周德宏. 两两NQD列的一个强大数律, 武汉理工大学学报, 2010, 32(19): 193~196

  118. 陈晓林, 吴群英, 邓光明, 两两NQD的完全收敛和强大数定律, 桂林理工大学学报, 2010, 30(2): 321-323

  119. 付艳莉, 吴群英, LNQD序列几乎处处中心极限定理, 桂林理工大学学报, 2010, 30(4): 637-639

  120. 谭成良, 吴群英, 贾贞, 孟凡宇, 混合序列的强大数律, 桂林工学院学报, 2008, 28(2): 285~288

  121. 鄢寒, 吴群英, 孟凡宇, 混合序列的完全收敛性和强大数律, 桂林工学院学报, 2009, 29(3): 419~422.

  122. 鄢寒, 吴群英, 王叶超, 两两NQD阵列行和的若干极限定理, 数学的实践与认识, 2010, 40(23): 155~160

  123. 居先祥, 吴群英, 关于同分布两两NQD列的Jamison型加权乘积和的强大数律, 桂林工学院学报, 2008, 28(3): 438~441.

  124. 叶大相, 吴群英, 随机元序列几乎处处中心极限定理的推广, 吉林大学学报(理学版), 2011, 49(2): 251-254.

  125. 兰冲锋, 吴群英, 叶大相, 同分布两两NQD序列部分和之和的强大数律, 桂林理工大学学报, 2010, 30(4): 640-643

  126. 谭成良, 吴群英, 何燕梅, 行为 混合阵列加权和的收敛性, 数学杂志, 2011, 3(1): 103-108

  127. 谭成良, 吴群英, 混合阵列行加权和的 收敛性, 广西科学, 2007, 14(3): 233~235

  128. 谭成良, 吴群英, 胡光辉, 混合序列的不变原理, 广西科学, 2007, 14(4): 360~361

  129. 黄海午, 吴群英, 王瑶, 两两NQD列的收敛性质, 广西科学, 2007, 14(2): 122~123, 127

  130. 黄海午, 吴群英, 王瑶, 两两NQD列的一个弱大数定律注记, 湖南文williamhill体育入口注册学报, 2007, 19(1): 34~35, 43

  131. 崔昊英, 吴群英, 黄海午, 关于不同分布 混合序列的加权和的强稳定性, 广西科学, 2007, 14(1): 33~34, 43

  132. 居先祥, 吴群英, 胡光辉, 不同分布两两NQD的强大数定律, 广西科学, 2007, 14(4): 357~359

  133. 居先祥, 吴群英, 胡光辉, 混合序列的Cesaro强大数定律的收敛速度, 广西民族大学学报, 2007, 13(2): 55~58

  134. 胡光辉, 吴群英, 居先祥, 混合序列的几乎处处收敛性, 广西科学, 2008, 15(2): 128~130, 137

  135. 李春红, 吴群英, 多元统计方法在分析广西区各市经济指标中的应用, 现代经济, 2007, 6(8): 30~32

  136. 李春红, 吴群英, 付艳莉, DN序列的中心极限定理, 广西科学, 2010, 17(1): 43~47, 51

  137. 孟凡宇, 吴群英, 辽宁城市发展的因子聚类分析, 现代经济, 2007, 6(8): 43~45

  138. 付艳莉, 吴群英, 两两NQD阵列加权和的收敛性, 广西科学, 2010, 17(1): 39~42.

  139. Yan Han, Wu Qunying, Meng Bing. Complete convergence and strong convergence for weighted sums of -mixing random sequences, Guangxi Science, 2009, 16(1): 38~40, 45.

  140. 鄢寒, 吴群英, 基于时序全局主成分分析的广西经济发展动态描绘, 广西科学院学报, 2008, 24(3): 168-170

  141. 袁文斌, 吴群英, 鄢寒, 我国全社会固定资产投资与经济增长关系的典型相关分析, 现代经济, 2008, 13: 107, 117.

  142. 付艳莉, 吴群英, 基于因子分析和聚类分析的山东省主要城市经济发展水平的综合评价, 科技信息, 2008, 34: 3~4

  143. 陈晓林, 吴群英, 两两NQD列的几乎处处收敛性, 广西科学, 2009, 16(3): 260~263.

  144. 叶大相, 吴群英, 稳定分布吸引域的几乎处处中心极限定理, 安徽工程科技学院学报, 2010, 25(3): 68~70.

  145. 简默, 吴群英, 彭先豪, 优化权重下 -混合序列部分和的几乎处处中心极限定理, 广西科学, 2010, 17(3): 200~201, 205

  146. 兰冲锋, 吴群英, 严云云, 我国各地农村居民人均消费支出的对应分析, 现代经济, 2008, 7(4): 53~55.

桂林理工大学williamhill体育入口注册  地址：桂林市雁山区雁山街319号  邮编：541006  电话：0773-3696613                        学院官微，扫码关注，获取最新信息